1. What is a Flux model?

Flux models provide an approximation to the solution of the [GLOSS]Radiative Transfer Equation[/GLOSS] ([GLOSS]RTE[/GLOSS]) within absorbing, emitting and [GLOSS]scattering[/GLOSS] media. The RTE is a formulation of the radiation transfer as a differential equation, which also includes an integral term (integro-differential equation). The RTE is a generalised equation of a monochromatic beam passing through a differential element (Fig. 1). It allows for:

q       Attenuation of the beam by absorption and scattering within the element,

q       Increase in intensity according to Planck’s law (see CF71)

q       Increase in intensity due to other radiation incident on the element and scattered in the direction of the beam according to the [GLOSS]scattering albedo[/GLOSS] for scattering.  This is represented by the integral term in the RTE. Scattering may also be [GLOSS]isotropic[/GLOSS] or non-isotropic.

Exact analytical solution of the RTE is limited to very simple cases. The solution of the RTE is complicated by the fact that radiation intensity is a function of both position and direction.

The basis of all flux models is to simplify the problem by approximating the directional variation of intensity. This is accomplished by subdividing the angular range into a small number of angles in each of which the intensity is assumed to be constant i.e. the intensity is uniform within a given solid angle. The RTE can then be written as a small set of differential equations in terms of average radiation intensities or fluxes. These can be solved given appropriate boundary conditions. The division of the 4p [GLOSS]steradians[/GLOSS] of solid angle does not have to be uniform.

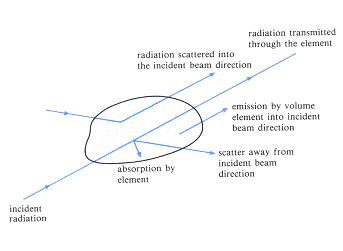
Fig. 1  The radiation energy balance on a monochromatic beam passing in a specified direction through a volume element in an absorbing, emitting and scattering medium.

Flux models differ from each other primarily by the number of discrete fluxes that are used to represent the continuous angular distribution of the radiation field.  Early versions were based on the so-called two- and four-flux models:

q       The two-flux approximation for one-dimensional problems represents the intensity by two fluxes F⁺ and F^– in the positive and negative coordinate directions. The RTE then reduces to a coupled pair of differential equations.

q       In multi-flux models (four-flux and six-flux), the intensity is resolved into positive and negative fluxes in the 2 or 3 coordinate directions respectively.

2. The Discrete Ordinate Flux model  

The Discrete Ordinate model (DOM) is a multi-flux model. Here, the integral term in the RTE is approximated by numerical quadrature (basically a weighted sum of terms that approximates to the integral) summed over each ordinate. Sometimes referred to as S-N approximations, referring to the number N of angular subdivisions, the DOM has been widely applied to 1-D  and 2-D cylindrical and rectangular problems. 

This method is flexible and can be accurate if enough directions are considered. It can account for absorption by gases as well as absorption and scattering by particles.  In the case of scattering, the integral term in flux models can be discretised according to a [GLOSS]phase function[/GLOSS], which allows for non-isotropic scattering.

The major advantage of the method is that it is compatible with numerical techniques for solving flow equations ([GLOSS]CFD[/GLOSS]). The method can suffer from a so called ‘ray effect’ however. In effect radiation is constrained to stream only along the chosen directions. This effect is worse for non-scattering (purely absorbing) media, but can be reduced by increasing the number of ordinates.

Sources

1.        Hottel and Sarofim, Radiative Transfer, McGraw-Hill, 1967.

2.       Selçuk N., ‘Evaluation of Flux Models for Radiative Transfer in Rectangular Furnaces’, Int.J.Heat Mass Transfer, vol. 13, no.7, pp. 1477-1482, 1988.

3.       Fiveland W.A., ‘Discrete-ordinates solutions of the Radiative Transport Equation for Rectangular Enclosures’, J.of Heat Transfer, vol.106, pp. 699-706, 1984.