• What are the properties of an isothermal free jet?

    Date posted:

    • Post Author

      espadmin


1. General

In some large industrial furnaces heated by axial diffusion flames it is found that the simple laws of the free jet may be applied directly to estimate flow and mixing (CF4; CF7) This Combustion File sets out the principal flow and mixing properties of isothermal free jets.

2. Principal properties of a free jet

An isothermal free jet issuing from a nozzle as shown in Fig. 1 into a calm and infinite atmosphere possesses the following noteworthy properties: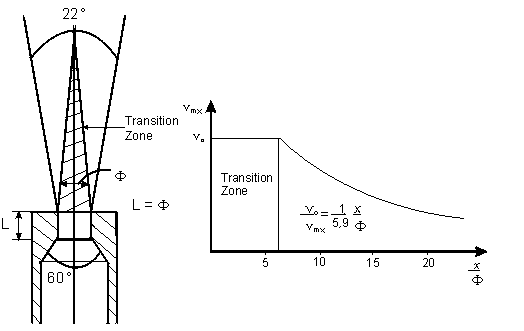

Figure 1: Variation of velocity and concentration on the axis of a jet as a function of the distance from the nozzle exit

  • The jet maintains a constant cone angle of about 22° whatever the nature or density of the fluid producing the jet.
  • In a zone near the nozzle exit, the axial velocity and concentration are equal to initial values (Note: although labelled transition zone in figure 1, this zone can be split into a potential core near the nozzle and a transition zone between the potential core and the fully developed free jet).
  • Beyond the transition zone (6 nozzle diameters) the axial velocity and concentration of jet fluid are inversely proportional to the distance from the nozzle (Fig. 1).

vmx = 5,9 v0 F/x      (1)


Cmx = 5,9 C0 F/x      (2)

where:


– v0 is the initial jet velocity (m/s),
– vmx is the axial jet velocity (m/s) at an axial distance x(m),
– C0 is the initial concentration of jet fluid (usually 1),
– Cmx is the fractional concentration of jet fluid at an axial distance x(m) and
– F is the initial diameter of the jet (m).



  • The radial velocity and concentration distributions remain similar to each other from one section of the jet to another (Fig.2)

C/Cmx = v/vmx = exp {-Ln2(r/r0,5)2}    (3)

where:

– r is the radial distance from the jet axis (m) and
– r0,5 is the radial distance (m) at which the velocity or concentration falls to half the axial value.



Figure 2: Free jet – radial distribution of velocity and concentration.



  • The jet entrains fluid from its surroundings. The mass flow Qmx of the fluid passing through a given section of the jet is proportional to the distance between this section and the nozzle exit.


  • Qmx = Qme + Qm = Kx(rxG)0,5      (4)

where:



– Qme is the mass flow of surrounding fluid entrained by the jet (kg/s),
– Qm is the mass flow of the jet leaving the nozzle (kg/s),
– K is a constant of proportionality,
– rx is the mean density (kg/m3) of the mixture (jet + surrounding fluid) at an axial distance x and
– G is the jet [GLOSS]thrust[/GLOSS](N).


3. Comment


Different authors have proposed other values for some of the constants used in this combustion file, including GEFGN themselves (see Combustion File 26). Rhine and Tucker (1) have given a useful review of this topic.

Reference


(1) J M Rhine and R J Tucker. Modelling of Gas Fired Furnaces and Boilers. 
McGraw-Hill 1991 (ISBN 0 07 707305 3)

Sources 


GEFGN, “Les proprietes du jet libre”, Rev, Gen. Therm. Fr., 133, January 1973

Acknowledgements


This Micrograph has been extracted from the “Recueil Des Fiches Techniques” published in the Revue Generale de Thermique.

We are unaware of the original author’s name. However we would like to thank the author and Gaz de France for their permission to use the information.

You may also like