1. Backround

With the enhanced capability and availability of mathematical techniques to model radiant heat transfer in furnaces and boilers, there is a requirement for more accurate data on the [GLOSS]emissivity[/GLOSS] of ceramic and metallic solids. Whilst standard compilations of emissivities and other radiative data^1-3 give a considerable amount of information this is often limited in the temperature range or composition of the material studied.  The nature and optical properties of the surface may change during use and this is especially the case with refractory materials in high temperature furnaces.  This problem has been intensified because of the interest in lining furnaces with ‘high-emissivity’ coatings and/or ceramic fibres or related low-density ceramic materials. There is often uncertainty about the effect of the [GLOSS]surface emissivity[/GLOSS] of these new materials on furnace performance.  There is also an increased interest in the use of radiation thermometers based around modern semi-conductor detectors, where the temperature deduced is a function of the assumed emissivity of the surface and accurate data is required.

This Combustion File outlines the mathematical basis for defining the surface emissivities of materials. Any self-consistent system of units may be used in the equations given below.

It concludes with general guidance on the values of emissivity for real surfaces commonly found in combustion systems.

Correlations and data to calculate temperature dependent values of surface emissivities of specific materials commonly found in combustion systems are given in linked Combustion Files (CF147, 148, 149, 223, 224).

2. The meaning of emissivity

In the analysis of radiative heat transfer, it is essential to be clear about the definition of emissivity because the term is often used ambiguously.  The emissivity of a surface or body is always defined as the ratio of the radiation emitted by the surface to the maximum possible, that is, from a black body at the same temperature.  However, since temperature, wavelength and direction may all affect this ratio, they should all be included in a fully comprehensive definition.  Arising from this requirement, a number of individual definitions may be encountered in the literature.

·          For radiation from a body at a particular temperature, the [GLOSS]directional monochromatic emissivity[/GLOSS] (or spectral emissivity) relates to radiation at a defined wavelength and direction (usually expressed as an angle, q, to the normal).

·          If radiation over the whole range of thermal wavelengths but in a specific direction is considered then the appropriate term is the [GLOSS]total directional emissivity[/GLOSS].

·          Similarly, if all the radiation emitted at a particular wavelength into the hemisphere beyond the surface is involved, the appropriate definition is that of the [GLOSS]monochromatic hemispherical emissivity[/GLOSS].

·          The value used in many analyses of radiative heat transfer in furnace enclosures is the simplest one.  It relates to radiation at all wavelengths and in all directions and is the [GLOSS]total hemispherical emissivity[/GLOSS].  It is the value used to multiply sT⁴ in the Stefan-Boltzmann expression, and it is often referred to simply as the emissivity.

·          Measurement of emissivity is frequently made with the surface orientated perpendicular to the radiometer, in which case the [GLOSS]normal emissivity[/GLOSS](total or monochromatic) is determined.

For real surfaces, the ratio of radiation emitted by the surface to that emitted by a black body at the same temperature is often called the [GLOSS]emittance[/GLOSS], although the definition is exactly the same as for emissivity.  In this text, emissivity will be used throughout because most industrial and research workers use it.

 

3. The Definition of Surface Emissivity

The emissivity of a surface may be defined as the ratio of the [GLOSS]radiance[/GLOSS] from the surface to that from a [GLOSS]black body[/GLOSS] viewed under identical optical and geometrical conditions and at the same temperature.  The total black body [GLOSS]radiation flux density[/GLOSS], or [GLOSS]emissive power[/GLOSS] E_b(T) at a fixed absolute temperature, T, is obtained from integration of the black body [GLOSS]spectral flux[/GLOSS], e_b(l,T), over all wavelengths l

 

This leads to the expression

 

where ó is known as the [GLOSS]Stephan-Boltzman constant[/GLOSS].

Based on the definition of emissivity, the total temperature dependent emissivity of a surface, e_t(T), may be written in terms of the black body emissive power and [GLOSS]spectral flux density[/GLOSS] of the surface, e(l,T), as

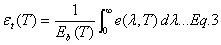
Integration of e(l,T) over the spectral band limits (l₁, l₂) will yield the spectral emissivity e_lj(T)

 

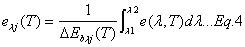
where lj is the nominal wavelength position defined by

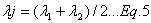
and DE_blj(T) is the black body band emissive power over the same wavelength range.

4. General guidance on surface emissivity

The emissivity of a surface varies with both temperature and wavelength for a metal.  The variation in wavelength follows theory for a radiating metal surface.  Non-conducting materials, such as ceramics, are more complex and can be further complicated because of surface roughness effects. Often surface finish (CF150) plays a major influence. In addition, measurements are very difficult to undertake accurately on an absolute basis.  Comparative values within one laboratory are often accurate but there can be substantial laboratory-to-laboratory differences due to the use of different techniques and different samples. 

Based on an examination of a large amount of data, the following general comments may be made regarding experimental values of surface emissivity:

·          The emissivity of clean metallic surfaces is small, being as low as 0.02 for polished gold and silver, although slowly increasing with temperature.

·          Oxidation of the metal surface markedly increases the emissivity, up to about 0.8 for heavily oxidised stainless steel.

·          The emissivity of conductors increases with temperature, whilst that of insulators will generally decrease or sometimes increase. 

·          Some metal oxides become semi-conductors at high temperatures, and these exhibit a U shaped emissivity curve.

·          The total emissivity of ceramics is generally around 0.6 but there is a considerable variation in the values.

·          The spectral emissivity of most refractory materials is quite low at wavelengths less than 5-6mm (typically less than 0.6) so that at higher temperatures over 1000K, the total emissivity tends to be lower at values around 0.4 to 0.5⁹.

·          Emissivity varies with temperature and wavelength because an increase in the temperature is accompanied by a decrease in the wavelength of that radiation according to the Planck distribution ^11,12,17.

·          The directional emissivity of a [GLOSS]diffuse surface[/GLOSS] is independent of direction and this is often a reasonable assumption for many real substances¹⁸.  Nevertheless, all surfaces exhibit some departure from diffuse behaviour and the general trends for the two special kinds of material discussed already, non-conductors and conductors, may be summarised as follows.

o          For conductors, 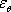  is approximately constant for q < 40°, increases up to about 80° and drops to zero at 90° (q = angle to the normal). 

o         For insulators 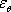 is roughly constant for q < 70° after which it drops sharply. 

The net result of these trends is that the hemispherical emissivity does not differ markedly from the normal emissivity, their ratio being between 1.0 and 1.3 for conductors and between 0.95 and 1.0 for insulators.

 

5. Experimental values of surface emissivity for common materials

Comprehensive tables listing the emissivity, e_0(T), of a wide range of materials as a function of temperature are given in three linked combustion files:

·          CF 147 – metals

·          CF148 – refractories, glasses and coatings

·          CF149 – carbons and coal ash

·          CF223 – glasses and ceramics

·          CF224 – coatings, paints, paper, porcelain and water

In these Combustion Files, emissivities are expressed as least squares polynomials fitted to data from the references listed in the Tables by the expression:

 

e_0(T) = a +10^-5bT + 10^-8cT² +10^-10dT³ … Eq.6

 

where T is the absolute temperature (K)

and a, b, c, d are fitted coefficients given in the tables. 

Acknowledgements

This work was funded in part by the UK Heat Transfer and Fluid Flow Service (HTFS) and part supported by the UK EPSRC. The information contained within this file was first published in the Journal of the Institute of Energy. 74, No 500 September 2001 (pp 91 – 99). The permission of the UK Institute of Energy to reproduce it here is gratefully acknowledged.

Sources

 

1.        TOULOUKIAN, Y.S. and DE WITT, D.P, Thermal radiative properties: Metallic elements and alloys, 1970, Vol. 7. TOULOUKIAN, Y.S. and DE WITT, D.P. Thermal radiative properties.  Nonmetallic solids, 1971, Vol. 8; in Thermophysical Properties of Matter, TPRC Data Series (edited by Touloukian, Y.S. and Ho, C.Y.) Plenum Press, New York.

2.       Handbook of Chemistry and Physics (60th Edition), CRC Press, Boca Raton, Florida, 1981.

3.       RATANAPUPECH, P. and BAUTISTA, R.G. Normal spectral emissivities of liquid iron, liquid nickel and liquid iron-nickel alloys.  High Temperature Science, 1981, 14(4) 269-283.

4.       WILLIAMS, A., HAMPARTSOUMIAN, E. and SIMMONS, B. Unpublished data.

5.       OSBORN, P.D. Handbook of Energy Data and Calculations.  Butterworth, London, 1985.

6.       FLETCHER, J.D. and WILLIAMS, A. Emissivities of ceramic fibre linings for high-temperature furnaces.  JInst.Energy, 377, 1984

7.       ELLISTON, D.G. GRAY, W.A., HIBBERD, D.F., HO, T-Y. and WILLIAMS, A. The effect of surface emissivity on furnace performance.  JInst.Energy, 1987, 155-167.

8.       GRAY, W.A., HAMPARTSOUMIAN, E., TAYLOR, J.M. and WILLIAMS, A. The role of radiation in determining the performance of gas-fired furnaces.  Proc. 1989 Int. Gas Res. Conf., Government Institutes USA Inc., 1989, Vol. III, 26-34.

9.       HAMPARTSOUMIAN, E. Spectral emittance measurements of furnace wall materials and coatings.  Ceramics in Energy Applications Conference, Sheffield, IOP Publishing Ltd., 1990, 149-157.

10.     JACKSON, J.D., YEN, C-C.  Measurements of total and spectral emissivities of some ceramic fibre insulation materials.  Ceramics in Energy Application, The Institute of Energy, London, 1994,159.

11.      JACKSON, J.D., AN, P. and PENA-MARCO, I. Measurements of the total and spectral emittance of permeable ceramic materials.  Proc. 4^th UK National Heat Transfer Conference, C510/132, I.Mech.E., 1995, 561-565.

12.     HOOGENDOORN, C.J. and WIERINGA, J.A. The effect of refractory emission on the energy efficiency of high temperature gas fired furnaces.  VDI Beridte, 1989, 765, 133-141.

13.     FISHER, G. Ceramic coatings enhance performance engineering.  Ceramic Bulletin, 1986, 65(283).

14.     WIERINGA, J.A. Spectral radiative heat transfer in gas-fired furnaces. PhD Dissertation, Technishe Universiteit Delft, 1992.

15.     SOLOMON, P.R.  Extension of emission-transmission techniques to particulate samples using FTIR.  Combustion and Flame, 1986, 66(47).

16.     Compilation of research data taken from: WALL, T.F. and BECKER, H.B. Total absorptivities and emissivities of particulate coal ash from spectral band emissivity measurements.  Journal Engineer for Gas Turbines and Power, 1984, 106, 771; GOODRIDGE, A.M. and MORGAN, E.S. JInst.Energy, 1971, 207. and Williarns, A. Unpublished data, 1988.

17.     KHAN, Y.U., LAWSON, D.A. and TUCKER, R.J. Analysis of radiative heat transfer in ceramic-lined and ceramic-coated furnaces.  JInst.Energy, 1998, 71, 21-27.

18.     HOTTEL, H.C. and SAROFIM, A.E. Radiative heat transfer.  McGraw Hill, New York, 1967.

19.     BENNET, H.E. and PORTEUS, J.D. J.Opt. Soc. Am., 1961, 51,123.

20.    GRAY, W.A. and MÜLLER, R. Engineering calculations in radiant heat transfer, Pergamon, 1974.

21.     DE WITT, D.P. and BERNICZ, R.S. Temperature, It’s measurement and control in science and industry, 4, 1 (Reinhold Publishing), 1972

22.    BRADLEY, D. and ENTWISTLE, A.G. The total hemispherical emittance of coated wires.  Brit. J. Appl. Phys., 1966, 17, 1155-1164.