1. What is a black body?

A [GLOSS]blackbody[/GLOSS] is a perfect absorber of incident radiation. Whatever the wavelength of incident radiation, no thermal radiation is reflected from the surface of a black body. A blackbody also emits the maximum energy possible for any given temperature.

Only a few substances such as carbon black approach the properties of a blackbody. Most surfaces, even many that appear black, are not perfect absorbers or emitters of thermal radiation.

2. How much radiation is emitted from a black body?

The energy emitted from a blackbody surface varies with wavelength. As the body gets hotter, more energy is emitted at shorter wavelengths. Above about
600°C, there is sufficient energy emission within the visible waveband of the spectrum (0.38-0.76

mm) for the surface to appear red. Planck first derived the relationship between energy emission and wavelength in 1900 from quantum atomic theory. The monochromatic [GLOSS]emissive power[/GLOSS] of a black surface (E_b,_l)
at temperature
T(°Kelvin) is given by:

where

c₁ = 3.74×10⁸ Wmm⁴m^-2
c₂ = 1.4388×10⁴

mm.K
and l is in micron
(mm) and E_b,_l is in
Wm^-2mm^-1

The [GLOSS]spectral emission[/GLOSS] from a black body is plotted in Figure 1 for two temperatures. For a body between 500 and
1500°C more than 98% of the radiant energy falls in the industrially useful near infra-red waveband
(0.76-25mm). The wavelength corresponding to the peak radiant flux is inversely proportional to temperature T(K) and is given by Wien’s displacement law:

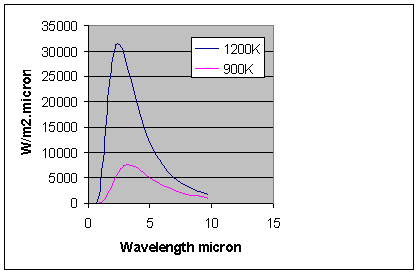
Figure 1. Radiant flux from a black body as a function of wavelength.

3. The Stefan-Boltzmann equation

Integration of the Planck equation over all wavelengths leads to the well known Stefan Boltzmann equation for [GLOSS]total radiation[/GLOSS] exchange from a black body surface:

where,

s
= the Stefan Boltzmann constant = 5.6687×10^-8 Wm^-2K^-4
E_b is the total energy emission per unit area over all wavelengths from a point on a black surface to all directions in the hemisphere above it (i.e. into
2p[GLOSS]steradians[/GLOSS] of solid angle)

4. An example

The outside surface of a furnace wall is at 120°C. What is the rate of heat loss from the surface assuming it approximates to a black body? Be careful first to convert temperature to degrees Kelvin ( T(K) =
T(°C)+273.0)

E_b = 5.6687×10^-8 x (120+273)⁴ = 1352W/m²

Sources

Thermal Radiation Heat Transfer, Robert Siegel & John R.Howell, 3rd Edition,
1992, Hemisphere, ISBN 0891162712