1. Background

Pulverised solid fuels such as [GLOSS]coal[/GLOSS] or [GLOSS]petroleum coke[/GLOSS]s are widely used today in various types of boilers and furnaces. The modelling of the associated combustion processes is of interest both for particle burnout times, and for understanding and predicting the formation of gas phase pollutants.

If one focuses on a single particle, the combustion process can be described in the following simplified way. On heating the particle undergoes a thermal degradation called [GLOSS]devolatilisation[/GLOSS]. During this phase, the fuel particle will release [GLOSS]volatile matter[/GLOSS], and a solid carbonaceous residue – called [GLOSS]char[/GLOSS] – is left.  On the one hand the volatile matter will oxidise, releasing part of the total energy of combustion. On the other hand, the char residue will oxidise, producing the remainder of the energy. This part of the combustion process is particularly interesting since char oxidation releases 40% to 98% of the total energy amount.

It is particularly important to know if the char particle will ignite or not. In this combustion file, an ignition criterion for a single char particle is described. It is based on comparing the rate at which heat is generated by the particle combustion with the rate at which it loses heat to the surroundings, both as a function of the particle temperature.

Depending on the particle properties and on its surroundings, each particle may or may not ignite, i.e. be brought to a temperature higher by several hundreds of °C than that of the surroundings. In addition, the rate of combustion is directly linked to the particle temperature, as are the carbon-in-ash content, and the physico-chemical nature of the [GLOSS]ash[/GLOSS].

2. Ignition criteria

The evolution with time of the temperature of a single particle can be calculated from the following energy balance:

 

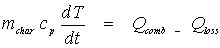  (Eq 1)

where:

·         C_p is the specific heat of the particle (J kg^-1 K^-1)

·         m_char is the mass of the particle (kg)

·         Q_comb is the rate of heat release by the oxidation of char reaction (W)

·         Q_loss is the rate of heat loss from the particle by exchange with the surroundings (W).

·         t is time (secs)

·         T is the particle temperature (C)

 

A large number of thermal properties, structural properties and chemical properties of the particle on the one hand, and the surroundings of the particles on the other hand have an impact on Q_comb and Q_loss. Since these parameters will drastically change during the combustion process, solving this equation is a rather complicated task. Nevertheless, there is a very interesting way to examine the process, which consists in assuming that a pseudo steady state can be reached, at a time when the particles properties and surrounding conditions are known. As suggested for the first time by Semenov, the heat balance equation then simplifies to:

 

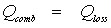  (Eq 2)

 

We consider here a small diameter particle: 50µm. As can be seen in Figure 1, the two curves present a single intersection point. The particle temperature stabilises at a value close to that of the surroundings, namely 1030°C.  This is a case where particle ignition does not occur.

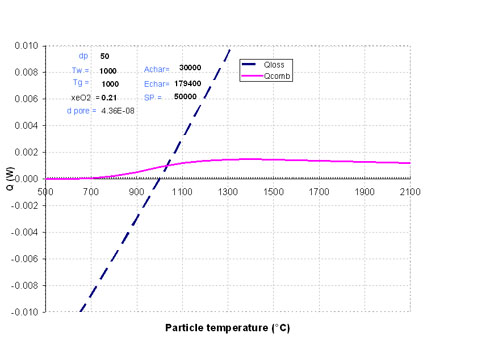
Figure 1 The case where the particle does not ignite

 

In the case of a large particle, e.g. 300 µm, the two curves in Figure 2 cross at a temperature much higher than that of the surroundings: 1660°C (Case 2).  Particle ignition occurs here.

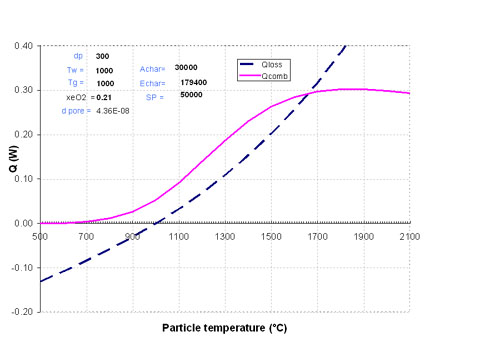
Figure 2: Case where particle ignition occurs

 

There is a particle diameter at which it is very difficult to predict whether ignition will occur or not. This is illustrated in Figure 3, where the particle diameter is 215µm and the gas and wall temperature 800°C: it is very difficult to define the crossing point, and consequently the equilibrium temperature. This consideration is very important: if one of the parameters of the problem happens to change, whether a particle property or a surrounding condition (temperature, oxygen content, heat/mass transfer conditions), the combustion regime can switch rapidly from ignited to not ignited. The particle can enter into an unstable combustion mode.

 

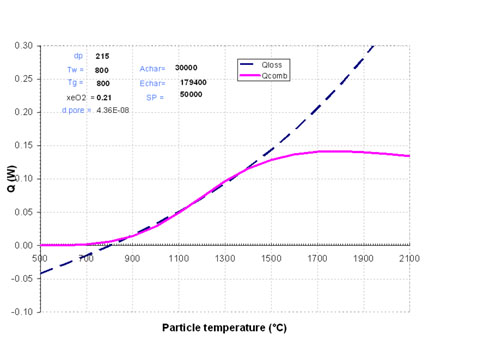
Figure 3: Unstable ignition condition

 

4. How do I determine Q_comb and Q_loss?

Any appropriate combustion and heat transfer models may be applied to determining Q_comb and Q_loss. Examples of the equations that can be applied, based on classical heat transfer and combustion phenomena, are given in CF258 and CF270.

5. Key parameters

There are a large number of parameters involved in the description of the particle combustion process. These parameters can be very different from one application to another. For instance:

Particle parameters

·         the diameter of the particle can range between less than 1µm to several mm;

·         the chemical reactivity of the char, or the Arrhenius pre-exponential factor, can vary in a ratio of 1 to 1000 for a given temperature;

·         the [GLOSS]porosity[/GLOSS] of the particle;

·         the reactive surface of the particle;

·         the [GLOSS]surface emissivity[/GLOSS] of the particle.

 

Parameters of the surroundings

·         the temperature of the surrounding gas, which can vary between 800°C and 2200°C;

·         the temperature of the furnace or of the walls, that define the radiative environment, can vary from ambient temperature to 2200°C;

·         the oxygen mole fraction vary between 0 and 20.8 % for a combustion in air, and can be higher in the case of oxygen enriched conditions.

 

As a consequence, it is not possible to predict the combustion regime for each particle size without calculations. Some general trends can nevertheless be established from the solution of a large number of conditions:

·         large particles are more likely to ignite than small ones;

·         increasing the char reactivity will favour particle ignition;

·         increasing the oxygen content of the surrounding gas will favour particle ignition.

6. Warning

Finally, we would like to point out that the results derived from this approach are to be considered as estimations more than precise calculations. All the predictions rely of course on the validity of the models used to calculate Q_comb and Q_loss.

Moreover, the “heterogeneous” ignition phenomena we are talking about can be coupled with “homogeneous” ignition phenomena, e.g., ignition of the volatile matter surrounding each particle.

As the oxidation reaction progresses, an ash layer can be formed at the surface of the particle, which will introduce an additional resistance to heat transfer and to oxygen transfer inside the particle. The combustion regime will be affected by these changes.

Also, due to the thermal inertia of the particle, a stable combustion regime predicted by this method might not be reached.

An extensive literature has been devoted to these phenomena. Some references are given below.

Sources

[1] Semenov N.N., Zur theorie des Verbrennungsprozess, Z Physik 1928; Vol 48, pp 571-582

[2] Essenhigh R.H., Misra M.K. and Shaw D.W. 1989, Ignition of coal particles  a review, Combustion and Flame, 1989, 77, pp 3-30

[3] B. Peters, Extinction of burning partices due to unstable combustion modes, Fuel Vol 81 (2002), pp 391-396

[4] A.S. Hull, P.K. Agarval, Estimation of kinetic rate parameters for coal combustion from measurements of the ignition temperature, Fuel 1998, Vol. 77, N° 9/10, pp 1051-1058

[5] T. Reichelt, T. Joutsenoja, H. Spielthoff, K.R.G. Hein, R. Hernberg, Characterization of burning char particles under pressurized conditions by simultaneous in situ measurement of surface temperature and size, 27^th Symposium (International) on Combustion/The Combustion Institute, 1998, pp. 2925-2932

[6] R. Hurt, Mechanisms of extinction and near-extinction in pulverized solid fuel combustion, 28^th Symposium (International) on Combustion/The Combustion Institute, 2000

[7] H. Katalambula, J-I. Hayashi, T. Chiba, K. Ikeda, K. Kitano, Mechanism of single coal particle ignition under microgravity condition, Journal of Chemical Engineering of Japan, 1997, Vol 30., pp. 146-153

[8]H. Katalambula, J-I Hayashi, T. Chiba, K. Kitano, K. Ikeda, Dependence of single coal particle ignition mechanism on the surrounding volatile matter cloud, Energy and Fuels, 1997, Vol. 11, pp 1033-1039

[9] J.C. Lee, R.A. Yetter, F.L. Dryer, Transient numerical modelling of carbon particle ignition and oxidation, Combustion and Flame, 1995, Vol. 101, pp 387-398

[10] Legrand B., Marion M., Chaveau C., Gökalp I. and Shafirovich EZ, Ignition and combustion of levitated magnesium and aluminium particles in carbon dioxide, Comb. Sci. Tech, 2001, 165, pp 151-174

[11] Morgan P.A., Robertson S.D. and Unsworth J.F, Combustion studies by thermogravimetric analysis, Fuel 65, 1986, pp 1546-1551

[12] Wall T.F., Gupta R.P., Gururajan V.S. and Zhang D-k, The ignition of coal particles, Fuel 70, 1991, pp 1011-1016

[13] Zhang D-k. and Wall T.F, Ignition of coal particles: the influence of experimental technique, Fuel 73, 1994, pp 1114-1119

[14] Zhang D-k. and Wall T.F. 1993, An analysis of the ignition of coal dust clouds, Combust. Flame 92, 1993, pp 475-48