-
How do I predict radiative heat transfer in industrial furnaces?
Date posted:
-
-
Post Author
dev@edge.studio
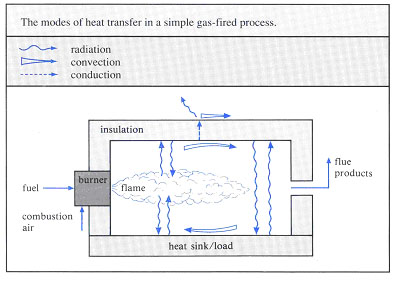
An accurate model of the thermal radiation in furnaces is important for predicting overall thermal efficiency, production rates, quality of the heated product, and pollutant emissions. The prediction of radiative transfer is complex due to the multidimensional and spectral nature of radiation. Thermal radiation exchange is the dominant mode of heat transfer in most furnaces and it depends on many factors including position, local temperature and composition. In order to make progress, a number of techniques have been developed which all introduce simplifying assumptions suited to the particular application or modelling approach. In a furnace enclosure, the flame and hot combustion gases emit radiation. The radiation is transferred to the load surface via a complex process including: q Direct radiation from the flame and combustion products q Direct radiation from other surfaces (walls) forming the enclosure q Radiation emitted by the gases, that arrives indirectly at the load surface after multiple reflections off the walls and other surfaces in the enclosure. This includes radiation which itself is reflected off the load and re-reflected back to the load. q Radiation that is partially reabsorbed (attenuated) by the gases or scattered by particles as it passes through the furnace space. Soot or mineral matter in the flame and combustion products may cause [GLOSS]scattering[/GLOSS]. The problem is further complicated by the fact that combustion gases are not grey. Simple models assume grey behaviour. More complex models include allowance for [GLOSS]non-grey gas[/GLOSS] behaviour. Furthermore, the combustion atmosphere may not be homogeneous in composition. Where flames extend into the furnace volume, then the composition of radiating components (CO2, H2O, carbon and particulate matter) can vary significantly with position as the air and fuel mix, and as combustion progresses. The different mechanisms of heat transfer in a furnace are illustrated in Fig.1. As well as modelling the internal radiative heat transfer described above, a complete model of a furnace should also take account of convective heat transfer (CF276) and conduction into and through the load and the furnace walls. Complex models may also include prediction of the turbulent fluid flow, mixing and chemical reaction taking place within the furnace. Fig.1 The heat transfer mechanisms in a typical fuel-fired furnace. Many different approaches to modelling radiation inside furnaces have been published. Broadly, the practical engineering methods can be grouped as follows: q The Zone method and related techniques [Hottel, Noble] q Flux models [Hottel, Selçuk, Fiveland] q q The Discrete Transfer method (DTM) [Lockwood, Docherty] Some, such as the flux models, are derived from astro-physics and the modelling of atmospheric radiation. Others, such as the ZONE method were developed specifically as furnace modelling tools. The choice of technique was once critically dependent on the availability of computers with sufficient speed and memory capacity. With modern processing capability this is no longer such a determining issue. The different techniques are described in more detail in CF271, 272, 273 and 274. The following table however, summarises the key features, advantages and disadvantages of these predictive methods. Model Type – Description Advantages Disadvantages The furnace volume is divided into isothermal surface and volume zones. Radiation heat balance equations are solved using radiation exchange factors between each zone pair. Can be applied as single zone or multiple zones. Single zone models can be computed by hand. Technique has been well validated and tested. Simple models do not require complex solution techniques. Can be applied to non-grey gases using a ‘[GLOSS]weighted sum of grey gases[/GLOSS]‘ model. Does not model non-homogeneous gas mixtures well. It is not compatible with the form of equations solved in [GLOSS]CFD[/GLOSS] models. If many zones are applied, then large numbers of exchange areas have to be computed and stored. Direct solution of the [GLOSS]Radiative Transfer Equation[/GLOSS] (RTE) by subdividing the directional variation into a small number of angles in which radiation intensity is assumed constant. Can be applied to non-homogeneous absorbing and scattering media. The form of equations is well suited to application and solution in CFD models. Results can suffer from errors due to ‘ray effect’. Uses random numbers to simulate and track individual beams of radiation through a furnace enclosure. Easy to apply to complex geometries. Can handle shadowing effects. Can be applied to model scattering, [GLOSS]Specular reflector[/GLOSS]s and directional and spectral wall properties. It is not compatible with the form of equations solved in CFD models. Statistical (random) errors can arise so there is no guarantee of convergence. Applies features of the above three methods: § divides space into volume and surface elements § divides the radiation into angular regions § tracks individual beams The DTM can handle non-homogeneous gases. Conceptually easy to apply. Adaptable to complex geometries. If applied with CFD models the models can share common volume and surface elements. Less accurate than the Zone method unless large numbers of elements are applied.
1. The need for radiation models
2. The types of radiation models
3. Which method should I use?
A Comparison of the Different Methods for Modelling Radiation Transfer in Furnaces
Zone Models
Flux Models
The DTM
Sources
1. Hottel H.C. and Sarofim A.F., Radiative Transfer, McGraw-Hill, 1967.
2. Noble J.J., ‘The Zone Method: Explicit Matrix Relations for Total Exchange Areas’, Int.J.Heat Mass Transfer, vol. 18, pp. 261-269, 1975.
3. Selçuk N., ‘Evaluation of Flux Models for Radiative Transfer in Rectangular Furnaces’, Int.J.Heat Mass Transfer, vol. 13, no.7, pp. 1477-1482, 1988.
4. Fiveland W.A., ‘Discrete-ordinates solutions of the Radiative Transport Equation for Rectangular Enclosures’, J.of Heat Transfer, vol.106, pp. 699-706, 1984.
5. Howell J.R., ‘Application of Monte Carlo to Heat Transfer Problems’, in Advances in Heat Transfer (T.F.Irvine and J.P.Hartnett, eds.), vol.5, Ac.Press, 1968.
6. Lockwood F.C., Shah N.G., Eighteenth Symposium (International) on Combustion, The Combustion Institute, 1981, pp 1405-1414
7. Docherty P., Fairweather M., ‘Predictions of Radiative Transfer from Non- homogeneous Combustion Products Using Discrete Transfer Method’, Combustion and Flame 71, 79-87 (1988).
You may also like
-
-
14th September 2003
-
