1. Background

There are a number of situations where it is required to know the rate at which heat is generated by combustion in a burning [GLOSS]carbonaceous[/GLOSS] particle as well as the rate at which the particle exchanges heat with its surroundings. The balance between these two will determine the time temperature history of the particle, and this in turn affects processes such as [GLOSS]char[/GLOSS] burnout, [GLOSS]slag[/GLOSS] formation and particle combustion stability.

A particular example of the way in which these two parameters may be used to evaluate an [GLOSS]ignition[/GLOSS] criterion for carbonaceous particles was described in a linked Combustion File (CF257).

Examples are given below of two sets of equations which may be used to calculate the rate of heat generation by the combustion reaction Q_comb, and the rate of heat exchange with the surroundings: Q_loss. The equations apply to a single spherical porous particle of carbon, in the presence of oxygen.

 

2. Heat released by the combustion reaction: Q_comb[W]

 

The rate of heat release by the oxidation reaction of a carbonaceous particle Q_comb (W) can be determined from equation (1) using the additional relationships given in equations (2) to (18) below:

 

             (1)

where:

m_char is the particle mass (kg)

t is time (s)

DH is the reaction heat (J.kg_C^-1)

 

2.1 The reaction heat DH

The reaction heat DH depends on the products of the reaction, which can be either CO or CO₂ or a mixture of the two, according to the molar relationship shown in equation (2).

 

Char   +  ( 1 – fr/2 ) O₂   ->   fr CO    +    (1-fr) CO₂                  (2)

 

where fr is defined in equation (5) below.

 

The mass fraction CO/CO₂ produced during the oxidation, r_mass , can be estimated from

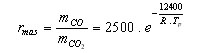                 (3)

where

R is the [GLOSS]universal gas constant[/GLOSS] = 8.314 J.mole^-1.K^-1

T_p is the particle temperature (K)

 

The heat released by the char reaction can be rewritten in terms of the parameter fr and the reaction heats for the formation of CO and CO₂ from the carbon in the char. The relationship is shown in equation 4:     

 

                (4)

 

with                                                     (5)

where

            M_CO2 is the molar mass of CO₂ (kg/mole)

            M_CO is the molar mass of CO (kg/mole)

2.2 The carbon reaction rate

The carbon reaction rate is expressed as:

                           (6)

 

in which the intrinsic reactivity k_char is expressed (kg.s^-1.m^-2.atm^-1)   

                                           (7)

where

            SP is the specific surface area of the char (m²/kg)

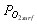            is the partial pressure of O₂ at the particle surface (atm)

            h is the effectiveness factor (-); see eq. (8)

            A_char is the [GLOSS]frequency factor[/GLOSS] for the char oxidation reaction (kg.s^-1.m^-2.atm^-1)

            E_char is the [GLOSS]Activation energy[/GLOSS] for the char oxidation reaction (J/mole).

 

The effectiveness factor h is the ratio of the effectively reactive surface to the total pore surface of the particle. It accounts for any limitation of oxygen diffusion inside the particle. For a spherical particle, and first order kinetics, we have

                                    (8)

           

It is calculated from the [GLOSS]Thiele Modulus[/GLOSS] f

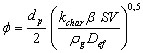                                    (9)

where

d_p is the diameter of the particle (m)

            r_g is the density of the gas (kg/m³)

            SV is the volumetric surface of the char (m²/m³)                   SV = r_p . SP

            b is the mass stoichiometric coefficient (kgO₂/kg_C)

 

The [GLOSS]effective diffusivity[/GLOSS] inside the particle D_ef  can be expressed as follows, if one takes into account both molecular diffusion and [GLOSS]Knudsen diffusion[/GLOSS] in the smallest pores

                                   (10)

where

             is the porosity of the particle (-)

            t is the [GLOSS]tortuosity[/GLOSS] of the particle (-)

            D is the [GLOSS]diffusivity[/GLOSS] of O₂ in N₂ (m²/s)

 

with the Knudsen diffusivity

                                   (11)

where    M_O2 is the molar mass of O₂ (kg/mole)

 

The average pore diameter d_pore (m) can be expressed as

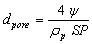      (12)

where r_p is the particle density (kg/m³)

 

and the porosity is given by

                                                (13)

where r_sol is the density of the solid fraction, or non porous carbon (kg/m³).

 

The oxygen flux F (mole 0₂/s) that is consumed by the reaction can be calculated from the carbon reaction rate, following the molar equation

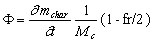                                 (14)

where M_C is the molar mass of carbon (kg/mole).

 

If this flux is transferred by convection, we can also write

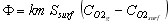                        (15)

where

            km is the O₂ mass transfer coefficient at the surface of the particle (m/s)

            S_surf is the particle outside surface area (m²)

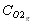            is the molar concentration of O₂ in the gas phase (mole/m³)

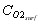            is the molar concentration of O₂ at the surface of the particle (mole/m³)

 

which enables us to calculate the oxygen concentration at the surface of the particle 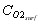, and to derive the oxygen partial pressure in  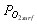eq. (6). The calculation describes oxygen transfer process outside the particle.

 

We also have

                                       (16)

where the particle [GLOSS]Sherwood number[/GLOSS]Sh_p is equal to the particle Nusselt number Nu_p (see also Section 3 below)

 

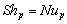  (17)

NB: since the calculation of h and of F require the value for the reaction rate, and the calculation of the reaction rate requires the knowledge of h and F, the previous calculations need an iterative procedure to converge to the solution.

3. Heat exchanged with the surroundings: Q_loss[W]

 

Taking into account the conductive/convective heat transfer and the radiative heat transfer, the heat flux exchanged between a spherical particle and its surroundings Q_loss (W) can be expressed

  

               (18)

where

            h is the [GLOSS]convective heat transfer coefficient[/GLOSS] at the particle surface (W.m^-2.K^-1)

            T_g is the gas temperature (K)

            T_p is the particle temperature (K)

T_w is the furnace wall temperature (K)

            e is the particle surface emissivity (-)

s_O is the [GLOSS]Stephan-Boltzman constant[/GLOSS] (5.67.10^-8 W.m^-2. K^-4 )

 

The particle surface convective heat transfer coefficient h can be calculated from

      

  (19)   

where l_g is the gas thermal conductivity (W.m^-1.K^-1)

 

The particle [GLOSS]Nusselt number[/GLOSS]Nu_p depends on the aerodynamic conditions.  If the particle is small and thus being conveyed in the gas stream without slip, Nu_p  =  2.  If there is slip between the particle and gas, then

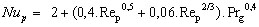(20)   

where Pr_g is the gas [GLOSS]Prandtl Number[/GLOSS] (dimensionless).

 

The particle [GLOSS]Reynolds Number[/GLOSS]Re_p is expressed as

                                          (21)

where m_g is the gas viscosity (dynamic ) (kg.m^-1.s^-1).

 

The slip velocity between the particle and the gas V_slip can be expressed as follows, in the case where the particle is submitted to gravity

                    

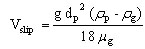    (22)

where r_g is the gas density (kg/m³).

 

NOMENCLATURE

 

A          frequency factor for carbon (char) oxidation             kg.s^-1.m^-2.atm^-1

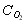     O₂ [GLOSS]molar concentration[/GLOSS] of the gas                           mole/m³

d           diameter                                                               m

D          diffusivity of O₂ in N₂                                           m²/s

E          activation energy                                                   J/mole

h           convective heat transfer coefficient                        W.m^-2.K^-1

k           [GLOSS]intrinsic reactivity[/GLOSS] of carbon                                  kg_C.s^-1.m^-2.atm^-1

km         mass transfer coefficient                                       m/s

m          mass                                                                     kg

M          molar mass                                                            kg/mole

P           pressure                                                               atm

Pr         Prandtl number                                                       –

Re         Reynolds number                                                     –

Sh         Sherwood number                                                    –

SP         specific surface area of the char                             m²/kg

SV        volumetric surface of the char                                 m²/m³  

(SV = r_p . SP)

T          temperature                                                          K

b          mass stoichiometric coefficient                               kgO₂/kg_C

r          density                                                                 kg/m³

       porosity of the particle                                          (-)

t           tortuosity of the particle                                          –

e           particle surface emissivity                                         –

l           thermal conductivity                                               W.m^-1.K^-1

m          viscosity (dynamic) of the gas                                  kg.m^-1.s^-1

h          effectiveness factor                                              –

f           Thiele modulus                                                       –

s₀         Stephan Boltzman constant = 5.67.10^-8                      W.m^-2.K^-4

DH        reaction heat                                                         J.kg_C^-1 

 

Constants

 

g           gravity                                                                 9.81 m.s^-2

R          universal gas constant = 8.314                                 J.mole^-1.K^-1

                                                                                      

Subscripts

 

char      char, or carbon ( C )

ext       surface of the particle

ef         effective, inside the particle

g           gas

p           particle

pores     pores

sol        solid fraction

surf      particle outside surface

w          furnace walls