1. Background

The [GLOSS]adiabatic flame temperature[/GLOSS] is one of a number of parameters that may be used to characterise some of the heat transfer and reaction characteristics of a fuel. During the IFRF G1 Furnace Trials [1], it was found possible to use the adiabatic flame temperature as a single variable against which the [GLOSS]thermal efficiency[/GLOSS] and [GLOSS]thermal NOx[/GLOSS] emissions from high temperature furnaces fired with [GLOSS]Blast Furnace Gas[/GLOSS] ([GLOSS]BFG[/GLOSS]) could be correlated (CF250, CF252).

This Combustion File recalls the basis for calculating the adiabatic flame temperature. It then sets out the results of such calculations as a quick and convenient graphical method for estimating the adiabatic flame temperature of blast furnace gas, including the effects of benefaction by means of:

·         [GLOSS]natural gas[/GLOSS] fuel enrichment

·       [GLOSS]oxygen enrichment[/GLOSS] of the combustion air

·         fuel and/or air preheat.

2. Adiabatic Flame Temperature

The adiabatic flame temperature T_f is calculated directly by equating the enthalpy of the fully reacted combustion products of a flame with the total heat input to the flame, including both the chemical and [GLOSS]sensible heat[/GLOSS] entering the furnace through the burner:

Q_in = Cp(T_f)*M_f*T_f    …………………..(1)

where:

o         Q_in is the total chemical and sensible heat input (W)

o         Cp(T_f) is the mean specific heat of the combustion products between ambient temperature and  T_f (J/kgC)

o         M_f is the mass flow of combustion products (kg/s)

Thus the adiabatic flame temperature T_f is given by:

T_f = Q_in/(Cp(T_f)*M_f) …………………..(2)

T_f is in fact the pseudo-adiabatic flame temperature, since equation (1) neglects the effect of [GLOSS]dissociation[/GLOSS] of combustion products that occurs at high temperatures. Levels of dissociation are very low below flame temperatures of 1600^oC, and this assumption has been found adequate for a low [GLOSS]CV[/GLOSS] gas such as BFG even when using benefaction levels as high as:

·         Air/fuel preheat to 500C

·         Natural gas enrichment to 10%

·         [GLOSS]Oxygen enrichment[/GLOSS] to 35% (by volume) oxygen in the [GLOSS]comburent[/GLOSS].

3. Graphical method of estimating adiabatic flame temperature

Although flame temperatures may be estimated directly from equation (2), such an approach requires the determination of a number of parameters characterising the total heat input and the [GLOSS]specific heat[/GLOSS] of the combustion products.  For a fixed fuel (BFG) and excess air level (10%), it is possible to make a quick estimate of flame temperature by using the alternative approaches of graphs given in Figures 1 and 2. The adiabatic flame temperature of a BFG flame is shown normalised against that of a natural gas flame with the same preheat conditions (expressed as the ratio of MW sensible heat added to the air and fuel to the total heat input in MW).

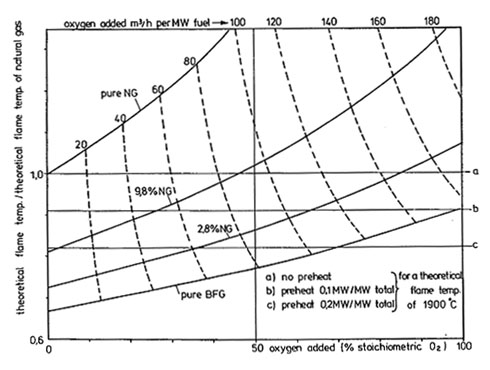
Figure 1. Pseudo-Adiabatic Flame Temperature as a function of oxygen enrichment for various BFG/NG mixtures – (10% excess air/oxygen)

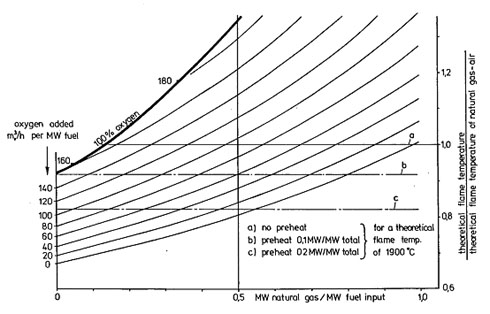
Figure 2. Pseudo-Adiabatic Flame Temperature as a function of natural gas and oxygen consumption (10% excess air/oxygen)

4. Examples of the use of graphical method

Considering Figure 1, for a BFG enriched with 2.8% natural gas, an adiabatic flame temperature equal to that of natural gas (1900C) can be obtained by the addition of 61m_o³/h oxygen per MW fuel and a preheat level of 0.2MW/MW. Without the oxygen addition, the adiabatic flame temperature of the same BFG flame would be 0.73/0.82 = 0.89 times the natural gas value of 1900^oC = 1691^oC.

Considering Figure 2, a BFG enriched with 5% natural gas, i.e. 0.05 MW natural gas/MW fuel input, and having no preheat or oxygen addition will have an adiabatic flame temperature of 0.68 times the natural gas value of 1900^oC = 1290^oC. Adding 0.1MW/MW preheat in either the fuel or the air would increase the adiabatic flame temperature to 0.68/0.92 = 0.74 times the natural gas value of 1900^oC = 1404^oC. On the same graph, it can be seen that oxygen addition of about 150m_o³/h per MW of heat input combined with an air or fuel preheat of 0.1MW/MW would achieve the same flame temperature as a natural gas flame (intercept of line b with the vertical axis through 0% natural gas).

5. Alternative representation of the effect of air preheat on flame temperature

The effect of air preheat on adiabatic flame temperature may be estimated directly from Figure 3.

Figure 3. Relative effect of fuel and /or air preheat on the pseudo adiabatic flame temperature (10% excess air/oxygen)

6. Limitations of the graphical method

The graphs given in Figures 1 and 2 have been determined from fits to data collected under the following conditions, and should be used with caution outside these ranges. In particular, higher levels of preheat than 500^oC on the air and fuel (corresponding to 20% of the total heat input to the furnace) and oxygen enrichment levels exceeding 35% oxygen by volume in the comburent may invalidate the assumption of negligible dissociation of the combustion products.

The experimental ranges are:

·         Total heat input 1.5 to 3 MW (fuel plus preheat)

·         Combustion intensity 60 to 120 kW/m³

·         Excess oxygen 10%

·         Air and/or fuel preheat up to 500^oC

·         Oxygen concentration in the comburent from 21% (air) to 50% by volume

·         BFG [GLOSS]Lower Calorific Value[/GLOSS] 2.3 to 3.1 MJ/kg

·         Natural Gas Lower Calorific Value 44 MJ/kg (7,2% inerts, 85% methane)

Acknowledgements

The author acknowledges the support and encouragement of Jean-Bernard Michel and Roy Payne during the adaptation of their original report to create this Combustion File.

Sources

[1] Michel J-B and Payne R. The use of blast furnace gas as a fuel in high temperature furnaces of the steel industry. Final report of the IFRF G1 trials, IFRF Doc No F01/a/100, March 1979.