-
How do I calculate the air required and flue gas composition for combustion of solid fuels?
Date posted:
-
-
Post Author
dev@edge.studio
1. Background
In order to engineer specific industrial [GLOSS]combustion[/GLOSS] processes it is necessary:
· To understand the thermal and combustion characteristics of the [GLOSS]fuel[/GLOSS]s available and the quality of their products of combustion (See Combustion Files (CF) 62 and 227).
· Further it is important to understand the characteristics of the [GLOSS]comburent[/GLOSS]s available (see CF61).
· To calculate the required comburent flow rate for given [GLOSS]furnace[/GLOSS] operating conditions.
· To calculate the exhaust or [GLOSS]flue gas[/GLOSS] composition and flow rate.
The present Combustion File details the elementary calculations required for the combustion of solid fuels.
2. Comburent requirements for combustion
Initially the oxygen requirements must be calculated.
The solid fuel considered is a [GLOSS]coal[/GLOSS], namely that specified in CF225.
Chemical reactions
Solid fuels mainly consist of the combustible elements C, H, and S. They also contain O, N, water and ash, which do not react in significant amounts with oxygen.
All gases are assumed to be perfect; therefore 1 kilo-[GLOSS]mole[/GLOSS] (kmole) of gas has a volume of 22.41 m3 at 1 atm and 273K ([GLOSS]STP[/GLOSS]).
The composition of solid fuels is usually given in weight fractions (kg/kg fuel), which are specified with the lower-case character of the substance, or in percent by weight.
As an example of a solid fuel, a typical steam coal is shown in Table 1 below. As indicated in CF225, the essential contributions to the calorific value of the fuel are from Carbon, Hydrogen and Sulphur.
|
Symbol |
C |
H |
N |
S |
O |
Ash |
Water |
|
% by weight |
76 |
5 |
1 |
2 |
3 |
6 |
7 |
|
|
|
|
|
|
|
|
|
|
Symbol |
c |
h |
n |
s |
o |
a |
w |
|
Mass fraction [kg/kg] |
0.76 |
0.05 |
0.01 |
0.02 |
0.03 |
0.06 |
0.07 |
Table 1: Analysis of a coal
The general combustion reactions are given in Table 2.
|
C |
+ |
O2 |
=> |
CO2 |
|
1 kmole |
|
1 kmole |
|
1 kmole |
|
12 kg |
|
32 kg |
|
44 kg |
|
12 kg |
|
22.41 m3 |
|
22.41 m3 |
|
1 kg |
|
1.867 m3 |
|
1.867 m3 |
|
|
|
|
|
|
|
2 H2 |
+ |
O2 |
=> |
2 H2O |
|
2 kmole |
|
1 kmole |
|
2 kmole |
|
4kg |
|
32 kg |
|
36 kg |
|
4 kg |
|
22.41 m3 |
|
44.82 m3 |
|
1 kg |
|
5.603 m3 |
|
11.205 m3 |
|
|
|
|
|
|
|
S |
+ |
O2 |
=> |
SO2 |
|
1 kmole |
|
1 kmole |
|
1 kmole |
|
32 kg |
|
32 kg |
|
64 kg |
|
32 kg |
|
22.41 m3 |
|
22.41 m3 |
|
1 kg |
|
0.700 m3 |
|
0,700 m3 |
Table 2: General Combustion Reactions
These numbers apply for complete (or [GLOSS]stoichiometric[/GLOSS]) combustion where the minimum required amount of oxygen (O2,min), is available.
Using air as the comburent instead of pure oxygen
For these calculations dry air is assumed; i.e. it contains no water.
Since dry air contains approximately 21% oxygen and approximately 78% nitrogen, 4.76 as much air as oxygen must be used to achieve complete combustion (1/0.21=4.76).
Fuels can also contain oxygen, which may reduce the amount of air required (also called the[GLOSS]stoichiometric air requirement[/GLOSS]).
In industrial combustion it is necessary to use more oxygen than required, the ratio O2/ O2,min of actually used oxygen to O2,min is called [GLOSS]excess air ratio[/GLOSS]and has the symbol l (Lambda), for stoichiometric combustion l = 1.
Calculation of the stoichiometric air requirement
It is now possible to derive an equation for Amin, the minimum volume of air per unit weight [kg] of fuel required for complete combustion. This equation uses the mass fraction of the fuel components as input parameters.

For the example from above this yields
Amin = (8.887)(0.76) + (26.67)(0.05) + (3.33)(0.02) – (3.33)(0.03)
Amin = 8.054 m3 dry air / kg coal at 1 atm and 273 K (STP)
3. Amount of flue gas produced
Flue gases consist of CO2, H2O(vapor), SO2, N2 and O2, this can be written as

From the reactions it can be seen that per kg of C, H and S in the fuel the following volumes of flue gases are formed:

The nitrogen emissions have two contributions: the nitrogen in the fuel and the nitrogen from the air:
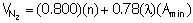
The volume of oxygen is the oxygen in the excess air:
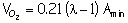
Calculating the amount of flue gases for the example given above with l = 1.3 gives
|
V = 1.867(0.76) + 11.205(0.05) + 0.700(0.02) + 0.800(0.01) + 0.78(1.3)(8.054) + 0.21(1.3-1)(8.054) |
|
V = 1.419 + 0.560 + 0.014 + 0.008 + 8.167+ 0.507 |
|
V = 10.675 m3 flue gas/kg fuel at 1 atm and 273 K (STP) |
4. Flue Gas Composition
To obtain the concentration of each component in the flue gas, the absolute volume of each species must to be divided by the total flue gas volume:
ratio [%] = 
Therefore the flue gas composition at l= 1.3 is
|
Species |
CO2 |
H2O |
SO2 |
N2 |
O2 |
|
% |
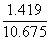
|
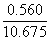
|
 |
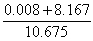

%
13.29
5.25
0.13
76.58
4.75
Sources
[1] Schramek, Taschenbuch für Heizung und Klimatechnik, Munich, 1999
[2] Perry, Perry’s Chemical Engineers’ Handbook 7th ed., 1997
