1. Background

The comprehension of [GLOSS]devolatilisation[/GLOSS] kinetics constitutes a first step towards the investigation of the entire coal combustion process, as flame characteristics (e.g. flame front position and stability, combustion efficiency) are partly governed by the release of [GLOSS]volatile matter[/GLOSS].

The conventional analysis of devolatilisation with [GLOSS]thermogravimetric analysis[/GLOSS] at the lab-scale can only fingerprint the fuel because the thermal conditions are far from those of practical applications and it is well known that devolatilisation kinetics change substantially when varying the heating rate.

In this context, the IFRF Isothermal Plug Flow Reactor (IPFR) is appealing as it is able to approximate the main characteristics of industrial furnaces in terms of heating rates and temperatures. Normally, the IPFR is used to make direct measurements of devolatilisation rates/levels and [GLOSS]char[/GLOSS] burnout. The IPFR could, however, potentially provide insight into kinetics. In this combustion file, we discuss the approach to using IPFR data to derive devolatilisation kinetics as well as issues that may affect the outcome. 

2. Derivation of devolatilisation kinetics

2.1 Standard procedure

The simplest devolatilisation model is the Single First Order Rate ([GLOSS]SFOR[/GLOSS]), according to which the rate of devolatilisation has a first-order dependence on the amount of volatiles remaining in the particle:

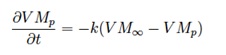
where

–       VM_p and VM_¡Þ are the actual and maximum volatile matter contents of the particle

–       k is the kinetic rate, that is defined by input of an [GLOSS]Arrhenius equation[/GLOSS] type pre-exponential factor A and activation energy E:

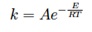
By assuming the particle temperature to be constant (equal to the reactor temperature) the SFOR model can be solved to give:

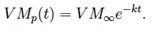
If experimental data on final volatile matter are available (VM_exp) for J sampling residence times t_j, a linear regression can be performed to evaluate the kinetic constant k_i from the runs at the i-th reactor temperature, according to:

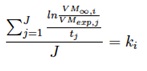
This can be done for different reactor temperatures in order to evaluate the Arrhenius parameters A and E according to:

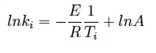
This procedure is simple and is often applied to derive devolatilisation kinetics from entrained flow reactors, but the simplifying assumptions made in this procedure, regarding the particle temperatures and trajectories, can result in errors in devolatilisation predictions. Those limitations are addressed in the advanced procedure.

2.2 Advanced procedure

There is some evidence and some issues which should be taken into account:

–       individual coal particles injected in the IPFR experience different paths and the [GLOSS]thermal history[/GLOSS]

–       the coal particles may not reach the reactor nominal temperature at all sampling locations.  This is especially true for devolatilisation experiments as sampling positions are located very close to the injection point in order to make measurements within a small time interval, typically 25-100 ms.

Hence, the procedure to derive kinetics should take into account:

–       of the real particle residence time, t, which is expected to be different from the estimated one (usually derived from the average IPFR gas residence time)

–       that the particle temperature Tp is not expected to be constant and may be different from the reactor temperature

–       that the entire particle cloud should be analysed.

Estimates of particle residence time and temperature can be provided by [GLOSS]CFD[/GLOSS] simulations of the IPFR experiments.  CFD can be used to derive t and Tp as well as their standard deviations (to characterise the particle cloud).

One approach is to use average values of t and Tp estimated for each experiment to numerically integrate the volatile matter equation and hence derive the SFOR parameters.

Alternatively, a simple but effective method could be to assume the particle temperature increases proportionally with the residence time t through the heating rate HR, estimated using CFD, as:

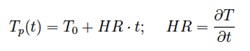
In this manner the volatile matter equation 

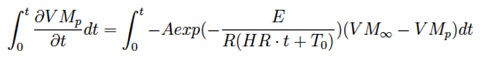
can be solved analytically to give

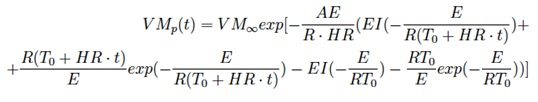
Here a fitting procedure (eg. non-linear least squares) may be used to evaluate A and E kinetic parameters.

3. Conclusions

The procedure outlined in this combustion file has been found to significantly improve the agreement between experimental and predicted conversion data. Conversely, the assumption of a constant particle temperature leads to a significant underestimation of the kinetic rates, especially at lower temperatures.

Sources

Author

Acknowledgements

The preparation of this Combustion File was supported by RELCOM; Reliable and Efficient Combustion of Oxygen/Coal/Recycled Flue Gas Mixtures ¨C a project undertaken with the financial support of the European Commission under FP7 Grant Agreement Number 268191.