-
What is fuzzy logic?
Date posted:
-
-
Post Author
dev@edge.studio
1. Introduction
Fuzzy Logic belongs to a class of artificial intelligence that provides a “convenient” way to map an input space or set of data to the corresponding outputs. A fuzzy logic model (also called a [GLOSS]fuzzy inference[/GLOSS] system) employs “common sense“ statements (encoded as “If-Then” rules) based on an understanding of the system behaviour whereas an artificial neural network (see combustion file CF46) uses [GLOSS]training data[/GLOSS] to generate an opaque, black-box model. In fuzzy logic the truth of any statement is “a matter of degree” and a fuzzy [GLOSS]membership function[/GLOSS] (MF) is used to relate an input to its appropriate [GLOSS]membership value[/GLOSS] (i.e. degree of membership), which can lie between 0 and 1. In contrast, standard Boolean logic uses either 0 or 1 to distinguish different states. Therefore fuzzy logic can be a very attractive technique for complex problems in the field of combustion, where it is often difficult to describe precisely the numerical relationships between process parameters [1].
2. Example of the Application of Fuzzy Logic to Combustion Systems
There has been an increasing utilisation of [GLOSS]biomass[/GLOSS] in industrial grate-fired boilers due to the need to reduce carbon emissions. One of the challenges to the more widespread adoption of the technology is the difficulty of burning cheap “poor quality” unprepared biomass materials with varying and relatively high moisture contents which can affect both the combustion and overall thermal efficiency of the boilers. These effects can be reduced by using a proportion of coal and high quality prepared biomass fuels such as wood pellets as a “support fuel” for the unprepared biomass. Most often, only the nominal moisture content of these biomass materials are known a priori. Consequently, in the absence of further fuel analysis, knowledge of the required optimum blend ratios can be difficult to determine due to the continuously changing moisture content of the unprepared biomass fuels. However, the degree of “wetness” of the biomass fuel can often be justified qualitatively by its physical appearance. The aim of this combustion file is to illustrate the principles of a fuzzy logic system by showing how it can be applied to determine the blend ratio. This uses a series of qualitative “linguistic” rules that can be formulated to describe the fuel blending process, as presented in the following sub-section.
2.1 Encoding the Problem
For simplicity, if numbers between 0 and 10 can represent the [GLOSS]Calorific value[/GLOSS] ([GLOSS]CV[/GLOSS]) and moisture content of fuel, what should the required percentage of support Fuel Mix (FM) be? In a fuzzy system, “If-Then” rules are used to formulate the conditional statements that comprise fuzzy logic. These rules then form the basis of the system behaviour. For this problem, the following simplified rule description may be applied, where each term in the brackets <. . .> comprises a fuzzy statement.
Antecedent Consequence
1. If <CV is High> and <moisture is High>, then <FM is Medium>
2. If <CV is High> and <moisture is Low>, then <FM is Low>
3. If <CV is Low> and <moisture is High>, then <FM is High>
4. If <CV is Low> and <moisture is Low>, then <FM is Medium>
2.2 Definition of the Fuzzy Sets
It is then necessary to define the [GLOSS]fuzzy set[/GLOSS] for each fuzzy statement in the antecedent and consequence of the rules via an appropriate membership function (MF). The choice of appropriate MFs is subjective and depends on the particular problem, and appropriate selection is vital in formulating a successful fuzzy inference system. The only condition a MF must satisfy is that it should have a value between 0 and 1 over the range of the input and output. Typical MFs for this example are shown in Figure 1. For instance, for the CV fuzzy set, as the CV rating of fuel increases from 0 to 10, the
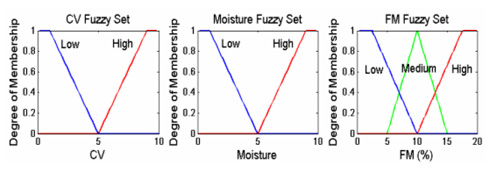
Figure 1: The Fuzzy Sets
degree of “Low” membership would decrease while the degree of “High” membership increases to its maximum of 1. Similar functions are then set up for the moisture and FM sets.
2.3 Fuzzy Inference
Mamdani’s fuzzy inference system [2] is the most commonly used fuzzy methodology, and this requires several steps as demonstrated in the following sub-sections.
Step 1- Fuzzification of the Inputs
This step transforms the input values by allocating a degree of membership between 0 and 1 to the fuzzy statements in the antecedent of each rule. The sequence in which each of the rules is accessed is not important. If there is only one part to the antecedent, then this is the only degree of support for the rule (See Figure 2(a)). It should be noted that it is the fuzzy statement(s) within the antecedent of each individual rule that dictate the membership function(s) to be used in the process of input fuzzification.
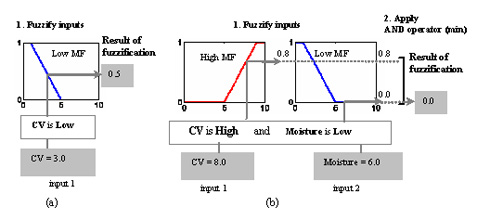
Figure 2: Inputs Fuzzification (a) single-part antecedent (b) multi-part antecedent
Step 2- Apply Fuzzy Operators
If there are multiple parts to the antecedent, as in this case, then fuzzy operators are applied to resolve the antecedent to a single number between 0 and 1 to yield the degree of support for the rule. The fuzzy equivalents of common binary-logic operators are listed in Table 1.
|
Binary-logic operators |
Fuzzy equivalences |
|
OR(A,B) |
max(A,B); probor(A,B) |
|
AND(A,B) |
min(A,B); prod(A,B) |
|
NOT(A) |
1-A |
Meanings
max(A,B) = maximum(A,B)
min(A,B) = minimum(A,B)
Probor(A,B) = A + B- A*B (probabilistic OR)
Prod(A,B) = A*B (Product)
Table 1: Fuzzy-Logic operators
Therefore for rule number 2, for instance, if the CV is rated as 8 and the moisture content as 6 the minimum of the two conditions yields a value of 0. This process is then repeated for all the rules in turn.
Step 3- Apply the Implication Method
A so-called implication technique is then applied to each rule, to “shape” the output (consequence) fuzzy sets using the single number outputs from the fuzzification of the antecedents. Two commonly used implication functions are the min (minimum) operation, which truncates the output fuzzy set, and prod (product), which scales the output fuzzy set. As an example, Figure 3 illustrates the result of implication when accessing rule number 2 with the “min” operation. It should be noted that it is the fuzzy statement within the consequence of each rule that dictates the membership function which is used in the process of implication.
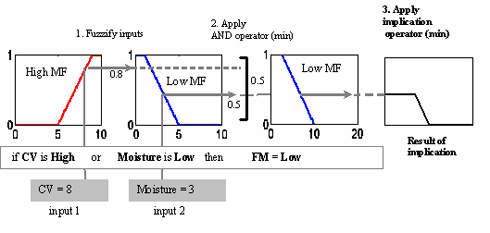
Figure 3: The Process of Implication
Step 4- Aggregation of the Outputs and Defuzzification
In a fuzzy inference system, the final decision is based on the reasoning derived from all of the rules. Therefore, the “transformed” output fuzzy sets described in step 3, which represent the outputs of each rule, must be combined in some manner into a single fuzzy set, see Figure 4. Three commonly used aggregation functions are: max (maximum), probor (probabilistic OR) and sum (sum of each rule’s output fuzzy sets). This aggregated fuzzy set is finally defuzzified in order to give a single output value, i.e. in this example the percentage of support fuel mix (FM). The most popular defuzzification method is the centroid calculation which computes the centre of area under the resultant combined curve; see Figure 4, which in this case is a blend of 4%.
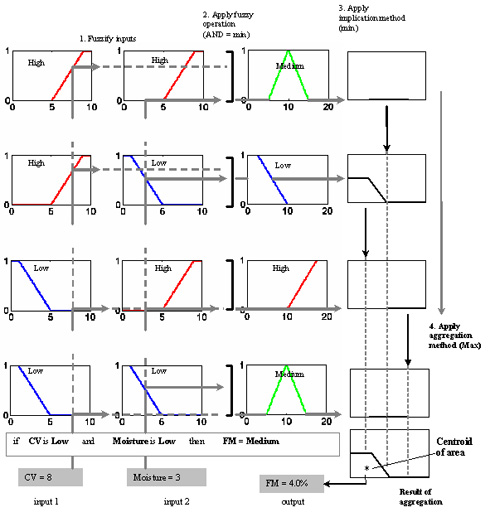
Figure 4: The Overall Fuzzy Inferences
3. Conclusions
The primary purpose of this Combustion File is to illustrate the basic concepts of fuzzy logic using a simplified fuel blending process. For a more complex combustion system such as in an incinerator [1], similar procedures would be applied to the 45 “if-then” rules using values for the six process variables to decide the settings for the manipulating variables such as the feeder speed. The real advantage of fuzzy logic lies in its ability to make decisions in ways which resemble human judgement and thus is tolerant of imprecise information.
Sources
[1] Ono, H., Ohnishi, T. and Terada, Y. (1989) Combustion Control of Refuse Incineration Plant by Fuzzy logic. Fuzzy Sets and Systems, 32(2): 193-206.
[2] MatLab® Fuzzy Logic Toolbox User’s Guide, The MathWorks, Inc., USA, 1998.
