-
What is the LES approach for turbulence modelling?
Date posted:
-
-
Post Author
dev@edge.studio
1. General
One of the rapidly improving methods available to “trouble-shoot” industrial combustion units, optimise and improve processes or test design changes, is the numerical modelling approach (CFD – computational fluid dynamics).
In these systems, fluids flow in the turbulent regime, which will have to be reproduced somehow in the numerical procedures. Strictly speaking, there is no definition on what exactly [GLOSS]turbulence[/GLOSS] is, and the scientific community has chosen rather to list some of its major characteristics. For further details see Combustion File,
CF110.
There are different degrees to the description of turbulence in flows for modelling purpose, like: Reynolds averaged Navier-Stokes equations (e.g., the k-ε model); large eddy simulation
([GLOSS]LES[/GLOSS]) or direct numerical simulation (DNS).
The first method is widely applied in the context of industrial furnace simulations. LES turbulence modelling is being more and more disseminated and appears to be promising in terms of progress of the quality of industrial turbulent predictions, but still requires too much computational time. DNS is appropriate for scientific research purposes and cannot be applied to complex engineering problems.
This CF describes the main characteristics of LES method to model turbulence.
2. The LES turbulence model
In the context of fluid flow analysis, turbulence is a three-dimensional, time-dependent, non-linear phenomenon wherein [GLOSS]vortex stretching[/GLOSS] takes place. A useful concept for discussing the main mechanisms of turbulence, is that of an “eddy”, which can be thought of as a typical turbulence pattern, covering a range of wavelengths, large and small, co-existing in the same volume of fluid. The actual modes of turbulence are eddies and high vorticity regions.
The small eddies are controlled by viscous forces and the large ones by the operating/boundary conditions, so that the features of turbulence strongly depend on the type of flow considered.
The main characteristics of turbulence is the transfer of energy to the smaller spatial scale that leads to the breaking down of large eddies to the small ones taking the form of an “energy cascade”.
The kinetic energy from the mean motion is extracted from the largest eddies and then transferred to the neighbouring smaller and smaller scale, creating larger and larger velocity gradients.
An increase in Reynolds number increases the difference between the largest eddies (low-frequency fluctuations) and the smallest eddies (high-frequency fluctuations). The large scales motions are generally more energetic than the small scale ones and their size and strength make them the most effective transporters of conserved properties.
Therefore, the idea is to do a 3D time-dependent numerical computation of the large scales turbulence and model the smallest scales that are nearly impossible to compute at present.
It is essential to define the quantities to be computed precisely: the velocity field that contains only the large scale components of the total field. This can be achieved by “filtering” (Leonard) the large (or resolved) scale field, which is essentially a local average of the complete field. The filtered velocity, in one-dimensional notation, is defined by:
![]()
where G(x,x’), the filter kernel (e.g. Gaussian), is a localised function. Every filter is associated with a length scale: Δ.
Broadly, eddies of size larger than Δ are large eddies, while those smaller than Δ, are small eddies which have to be modelled in this procedure.
When the Navier-Stokes equations for constant density (incompressible flow) are filtered, one obtains a set of equations very similar in form to the familiar Reynolds-averaged Navier-Stokes equations:
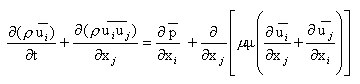
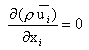
As the continuity equation is linear, filtering does not bring any significant modification:
It is important to note first that:
Since
![]()
and second, because the quantity on the left side of the inequality is not easily computed, a modelling approximation for the difference between the two sides of this inequality,
![]()
must be introduced.
In the context of LES, ![]() is called the subgrid scale Reynolds stress. The models used to approximate
is called the subgrid scale Reynolds stress. The models used to approximate ![]()
are called subgrid scale (SGS) models.
The SGS Reynolds stress is a local average of the small-scale field so that its model should be based on the local velocity field or, perhaps, on the past history of the local fluid.
The most commonly used SGS model is by proposed by Smagorinsky. It is a spectral eddy-viscosity and diffusivity model, based on the notion that: transport and dissipation are increased by the effects of the SGS Reynolds stress. By analogy to the viscosity in laminar flow and reasoning that the modelled part of the LES concept tackles small scales, a reasonable relationship could be formulated by:
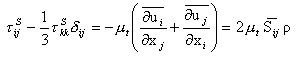
where
mt
is the eddy viscosity, ![]() is the mean strain rate and
is the mean strain rate and
![]() is the Kronecker delta. The form of the subgrid scale eddy viscosity can be derived by dimensional arguments and is:
is the Kronecker delta. The form of the subgrid scale eddy viscosity can be derived by dimensional arguments and is:
![]()
where CS is the model parameter, Δ is the filter length scale, and
![]() . Theories provide estimates of the constant. Most of these are valid only for isotropic turbulence but they agree that CS
. Theories provide estimates of the constant. Most of these are valid only for isotropic turbulence but they agree that CS
~ 0.2 . However, CS is not a constant and may be a function of Reynolds number and other non-dimensional parameters and may be different in different flows.
Some predictive discrepancies have been noticed when modelling for instance the near wall region or stratified flows (an-isotropic fluid structure) with the common form of the Smagorinski formulation. More elaborate subgrid-scale models have been developed to simulate specific complex applications.
Sources
Joel H. Ferziger, Milovan Perić, “Computational Methods for Fluid Dynamics”, Springer, 1997.
